1 Abstract¶
This technote describes the analysis and results derived from individual hardpoint breakaway tests conducted with the M1M3 surrogate. The notebook is located within notebooks_vandv GitHub repository. With all the steps guarded with reasonable timeouts, so problems are detected if hardpoint cannot travel to reach low or high limit switches, etc. If this test shows that the hardpoints do not work properly at the limits, this could be one of the blockers for the installation of M1M3 until it is solved.
2 Hardpoint Breakaway Test¶
The active support system of the M1M3 includes six axial hardpoint actuators in a hexapod configuration. [1]
These hardpoint actuators should minimize forces during slews at any TMA position and be kept under the breakaway limit. The breakaway limit for each hardpoint is in the range of -4420N to -3456N for retraction and 2981N to 3959N for extension. The following steps are performed during an individual hardpoint breakaway test are shown in test case LVV-T231.
As a summary:
Move hardpoint in negative (increasing tension) direction until the breakaway mechanism activates.
Move hardpoint in positive (increasing compression) direction until the breakaway mechanism activates.
Move hardpoint downwards (increasing tension) until the breakaway mechanism activates.
Move hardpoint back to its reference position.
Wait for the hardpoint to reach its reference position.
3 Requirements and Tickets¶
Associated JIRA tickets and requirements with this test:
LTS-88 LTS-88-REQ-0017-V-01: 3.7.5.1 Load Limiting Axial Breakaway Mechanism Displacement
LVV-11200 LTS-88-REQ-0015-V-01: 3.7.1.3 Hardpoint Displacement Repeatability and Resolution_1
LVV-11184 LTS-88-REQ-0024-V-01: 3.7.1.7 Hardpoint Axial Breakaway Repeatability_1
LVV-11208 LTS-88-REQ-0025-V-01: 3.7.1.8 Hardpoint Stiffness Limits_1
4 List of Hardpoint Breakaway Test¶
elevation |
azimuth |
Start Time |
SALIndex |
|---|---|---|---|
(deg) |
(deg) |
(YYYY-MM-DDTHH:MM:SS) |
|
0 |
-29.69 |
2023-05-30T21:26:51 |
100056 |
1 |
-29.69 |
2023-05-30T22:40:34 |
100057 |
5 |
-29.69 |
2023-05-31T00:00:10 |
100058 |
10 |
-29.69 |
2023-05-31T01:03:26 |
100059 |
20 |
153 |
2023-05-27T02:49:55 |
100036 |
20 |
153 |
2023-05-30T08:26:34 |
100047 |
40 |
153 |
2023-05-26T02:23:28 |
100034 |
89.95 |
153 |
2023-06-20T03:11:00 |
100038 |
90 |
-29.69 |
2023-05-31T05:44:14 |
100061 |
5 Hardpoint Test Result¶
5.1 A general results of HP Test¶
Todo
General results from HP test
More detailed description for results from HP tests.
5.2 HP Test at EL = 90deg¶
These are results from hardpoint breakaway tests when the TMA is positioned at EL=90 deg, AZ=-29.69 deg. Figure 1 shows that measured forces on the hardpoint 1 - 6 during the hardpoint axial breakaway test. Measured forces on all hardpoints look working properly because breakaway happened in the range of the requirement (tension: -4420 - -3456N, compression: 2981 - 3959N).
Todo
More detailed descriptions and explanations might be further needed.
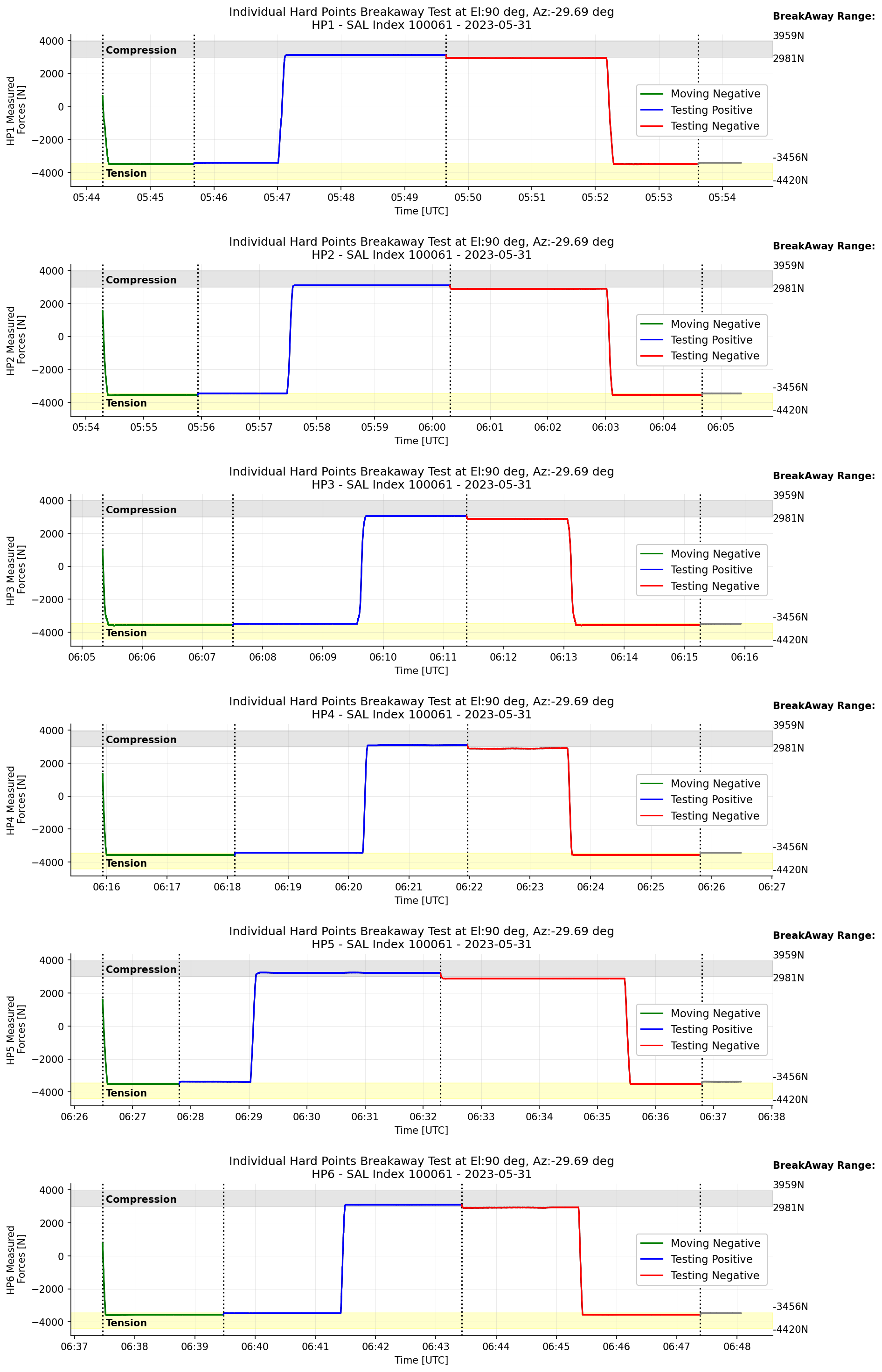
Figure 1 Transition of the measured forces on each hardpoint when the TMA is at el=90deg.¶
In Figure 2, there are the change of the measured force for each phase/status in the hardpoint breakaway test, moving Negative, testing positive, and testing negative, respectively. The stiffness of each curves are fitted with +-10 points from \(\Delta\)displacement = 0 \({\mu}m\). All stiffness slopes are shallower than specification (100N/\({\mu}m\)).
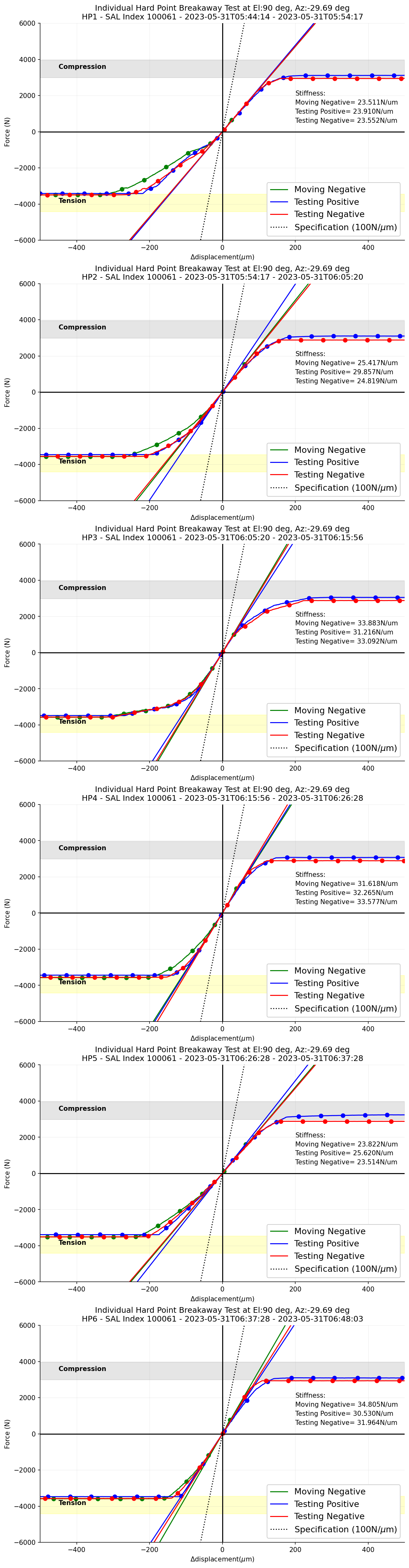
Figure 2 \(\Delta\)Displacement versus measured forces for each phase during the hardpoint breakaway test when the TMA is at el=90deg.¶
In order to check residual bumps during the movements of hardpoints, we adopted the error function (1) to fit the measured forces with respect to \(\Delta\)displacement for active phases when the hardpoints are moving toward negative and positive directions. As hardpoints breakaway limits for each direction are different, the functions at the positive and negative in x axes were fitted separately. The maxima of the bumps are about < 250N, which correspond < 10% of the measured forces.
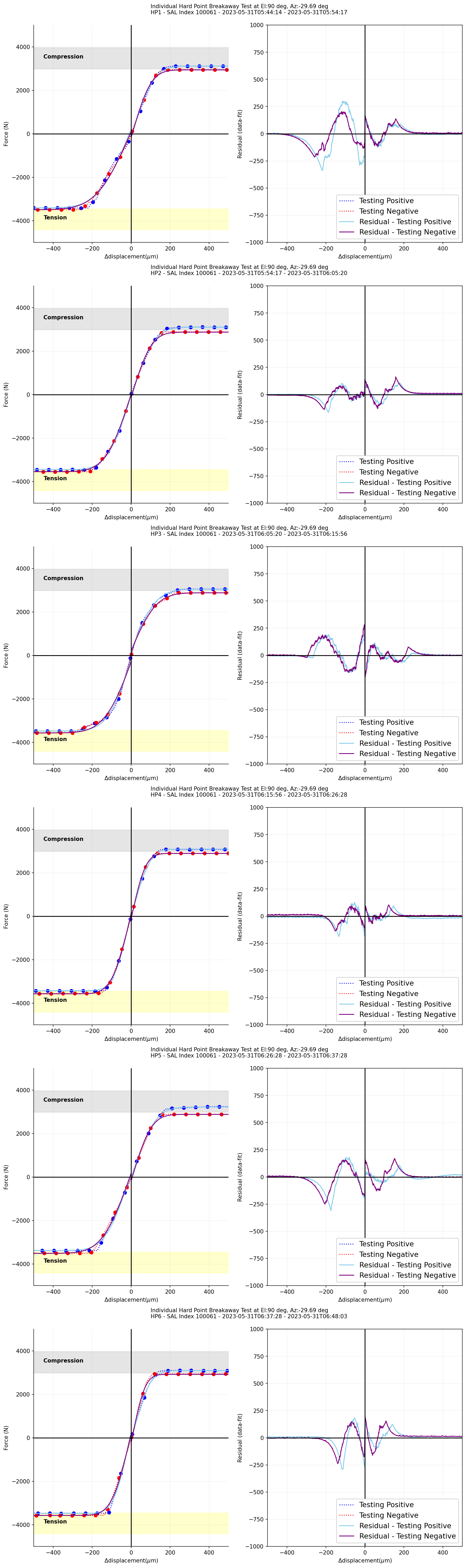
Figure 3 (Left) \(\Delta\)Displacement versus measured forces for each phase during the hardpoint breakaway test fit with error function (the TMA at el=90deg). (Right) The residual, a difference between data and error function, with respect to \(\Delta\)displacement¶
5.3 HP Test at el 0 deg¶
These are results from hardpoint breakaway test when the TMA was positioned at el=0 deg, az=-29.69 deg. In Figure 4, hardpoint 2 and hardpoint 5 were not moving to the positive direction. Hardpoint 1 and hardpoint 6 were both staying on the position for testing positive for a shorter period of time whereas hardpoint 3 and hardpoint 4 were staying on testing negative position for a shorter period time. This is because depending on the position of each hardpoint.
Todo
Reference cross check
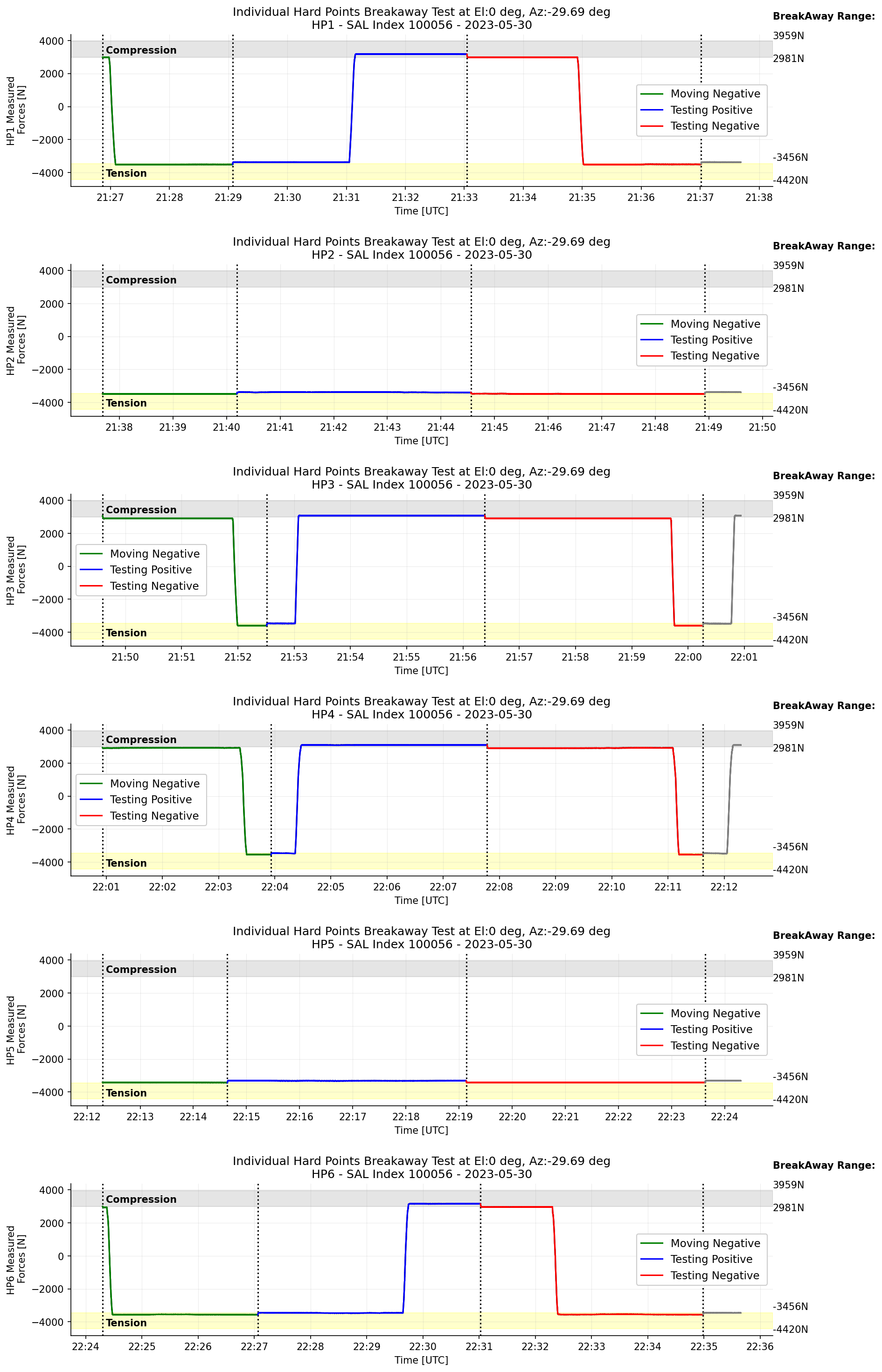
Figure 4 Figure 4. Transition of the measured forces on each hardpoint when the TMA is at el=0deg.¶
The stiffness of each curves are fitted from \(\Delta\)displacement = 0 \({\mu}m\) (Figure 5).
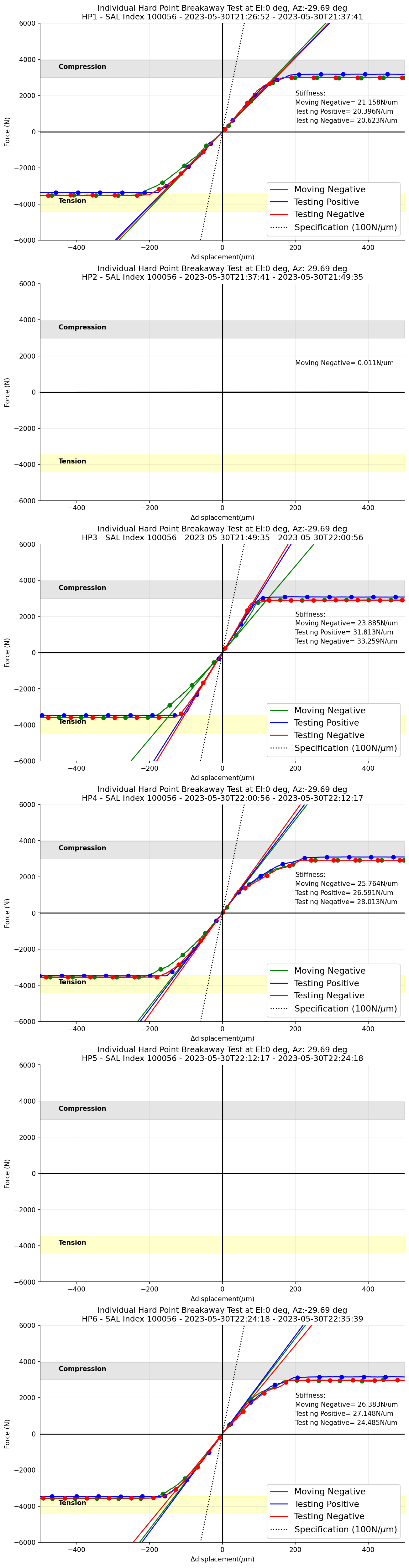
Figure 5 \(\Delta\)Displacement versus measured forces for each phase during the hardpoint breakaway test when the TMA is at el=0 deg.¶
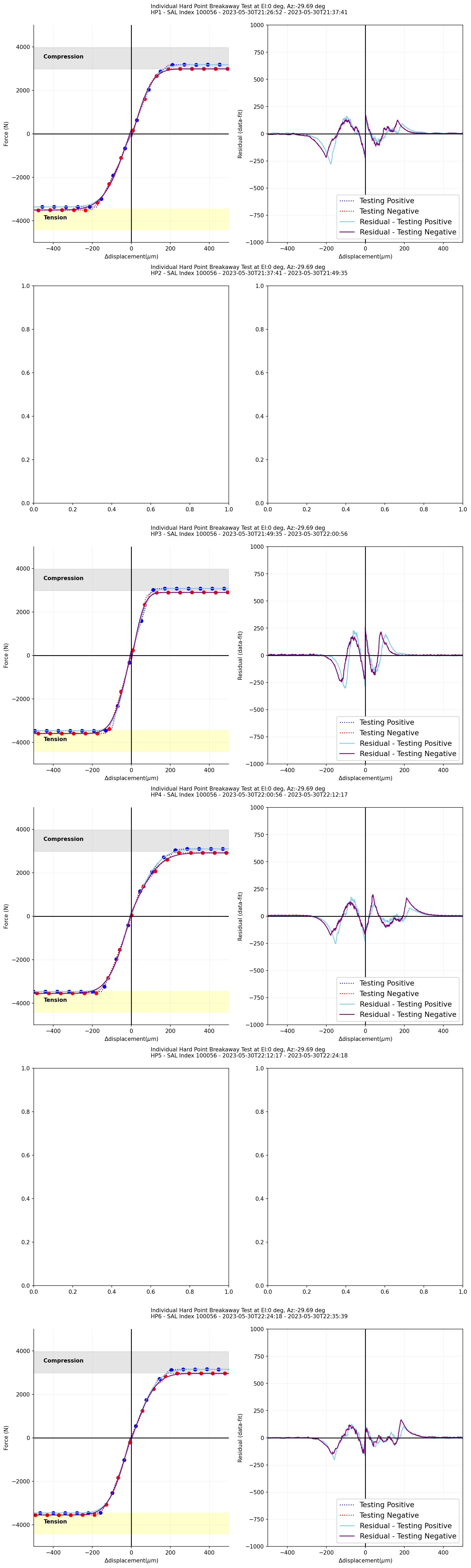
Figure 6 (Left) \(\Delta\)Displacement versus measured forces for each phase during the hardpoint breakaway test fit with error function (the TMA at el=0deg). (Right) The residual, a difference between data and error function, with respect to \(\Delta\)displacement¶
5.4 HP Test at el 40 deg¶
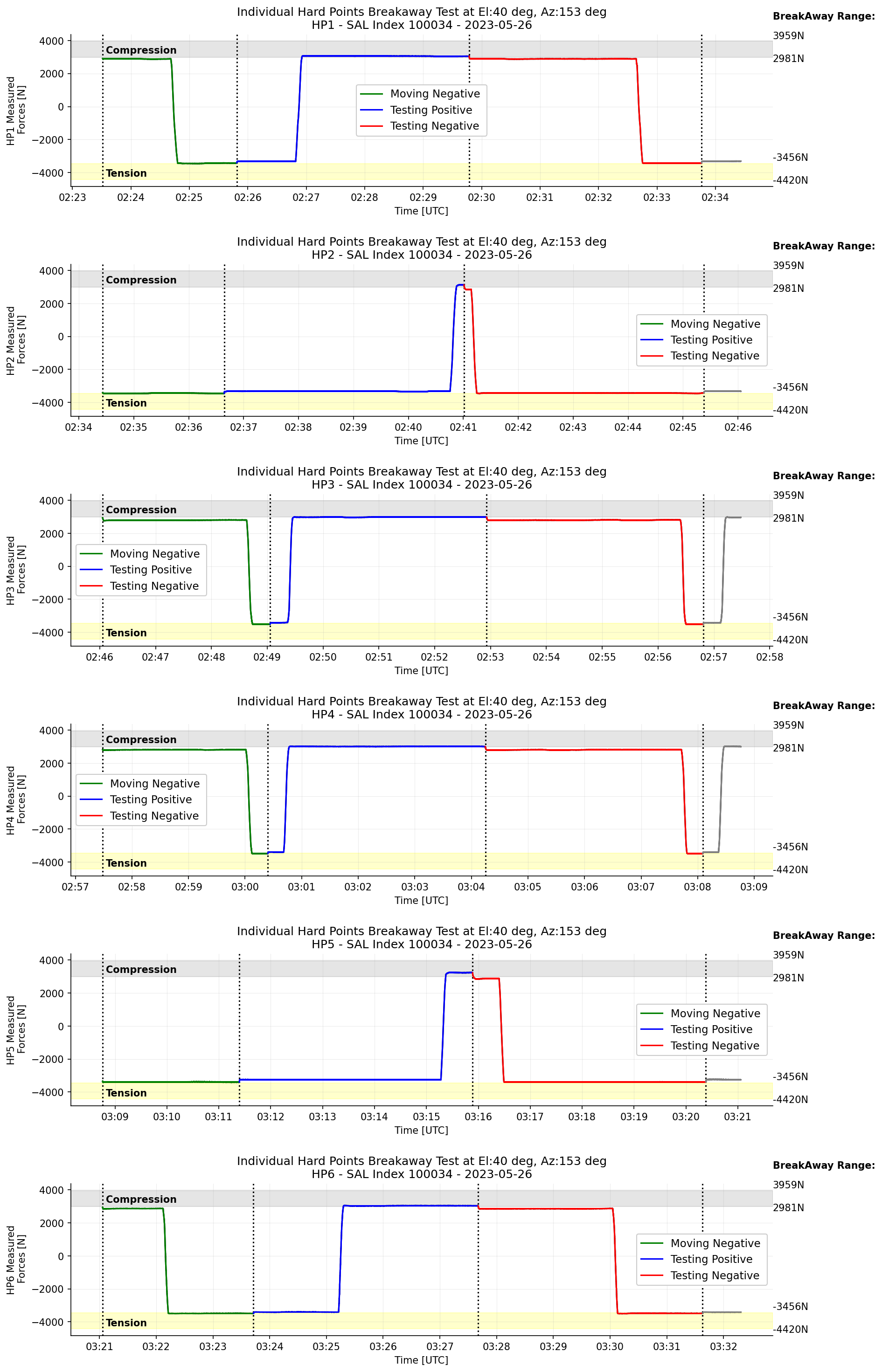
Figure 7 Transition of the measured forces on each hardpoint when the TMA is at el=40deg.¶
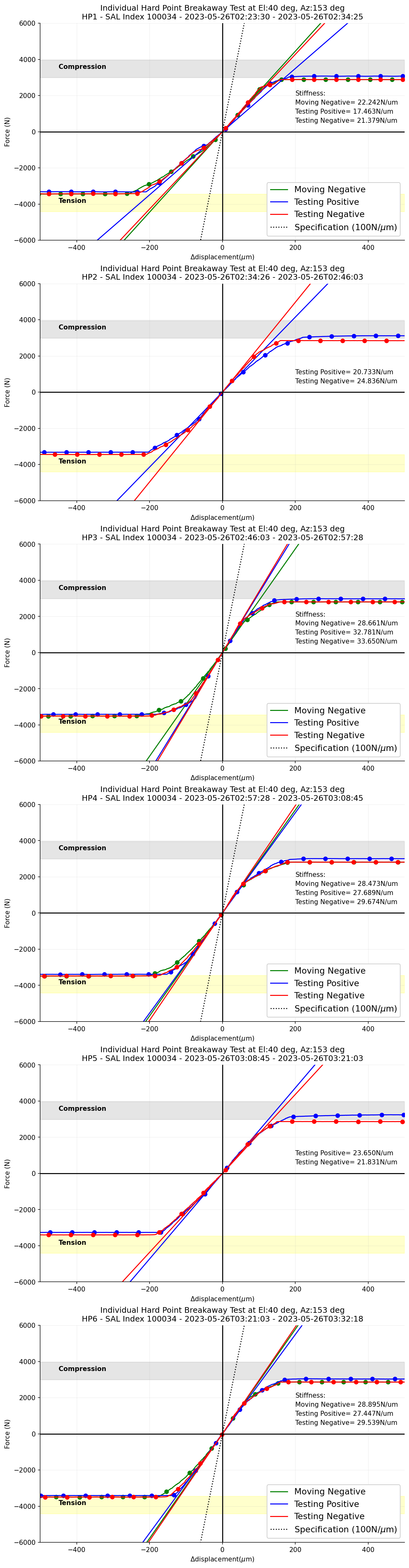
Figure 8 \(\Delta\)Displacement versus measured forces for each phase during the hardpoint breakaway test when the TMA is at el=40 deg.¶
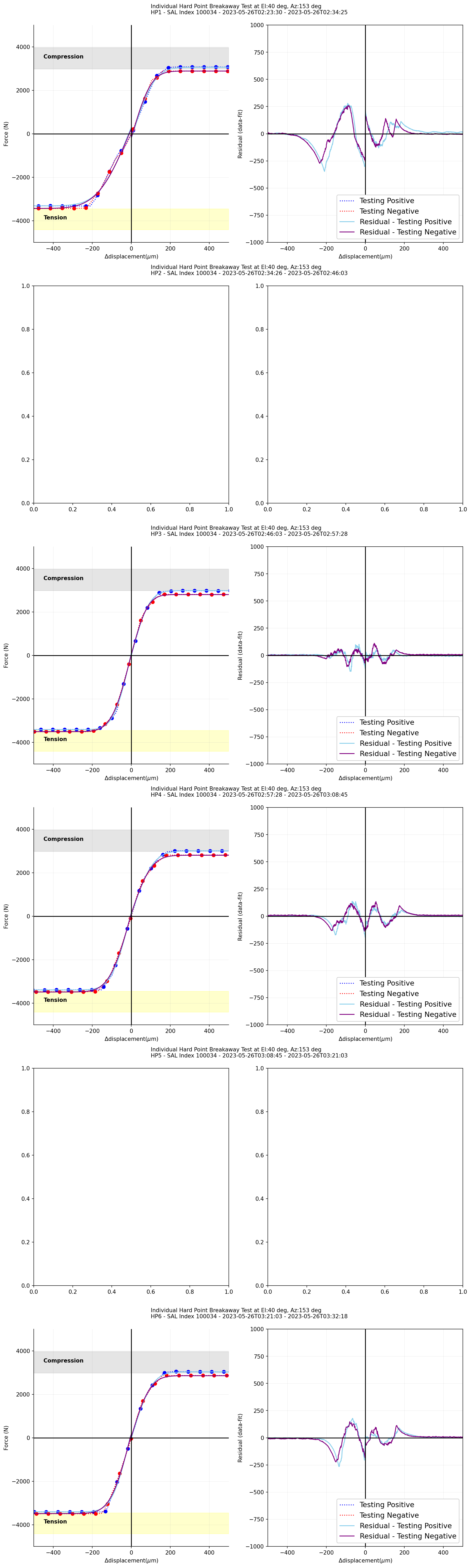
Figure 9 (Left) \(\Delta\)Displacement versus measured forces for each phase during the hardpoint breakaway test fit with error function (the TMA at el=40deg). (Right) The residual, a difference between data and error function, with respect to \(\Delta\)displacement¶
5.5 HP Test at el 20 deg¶
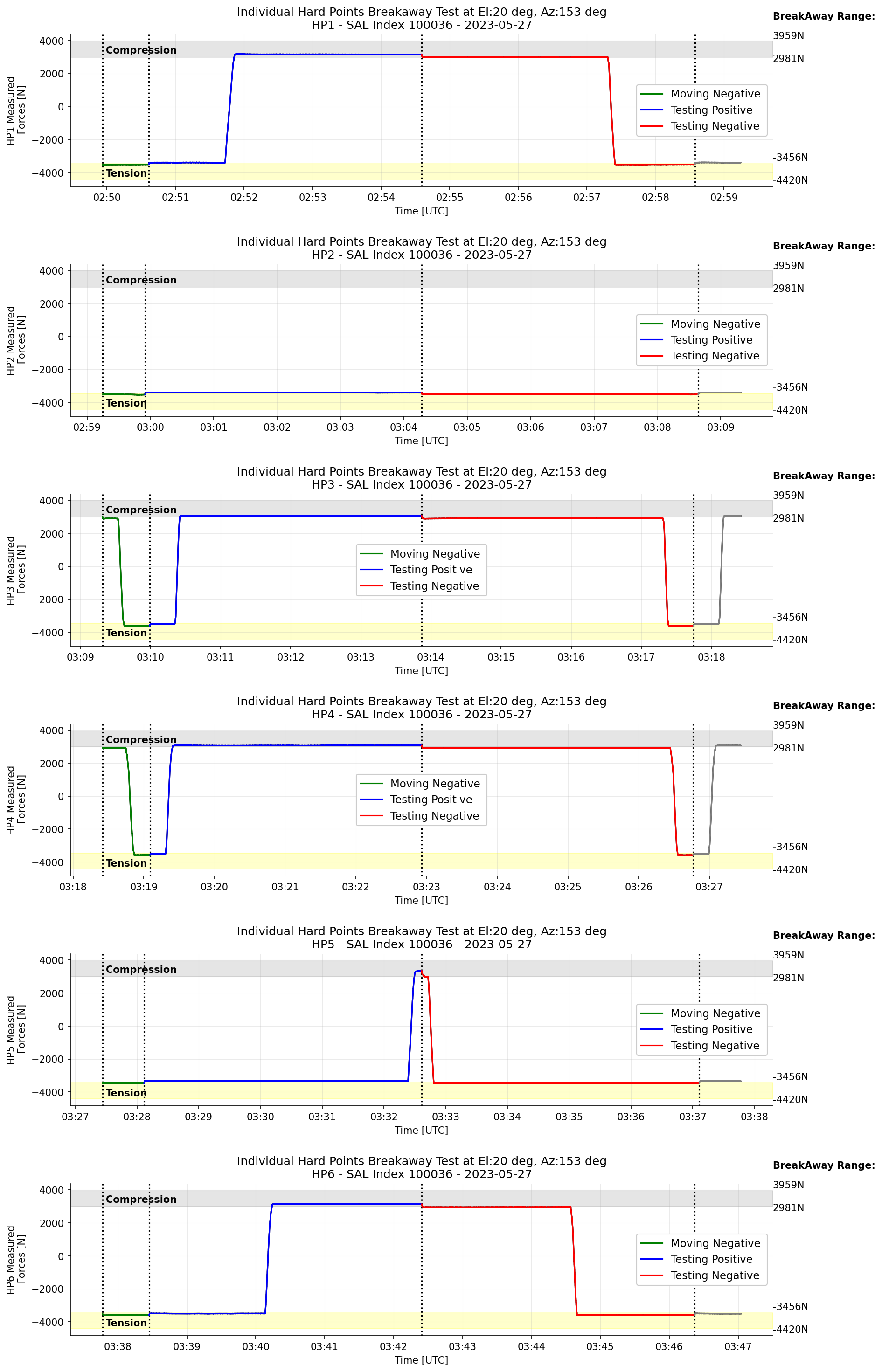
Figure 10 Transition of the measured forces on each hardpoint when the TMA is at el=20deg.¶
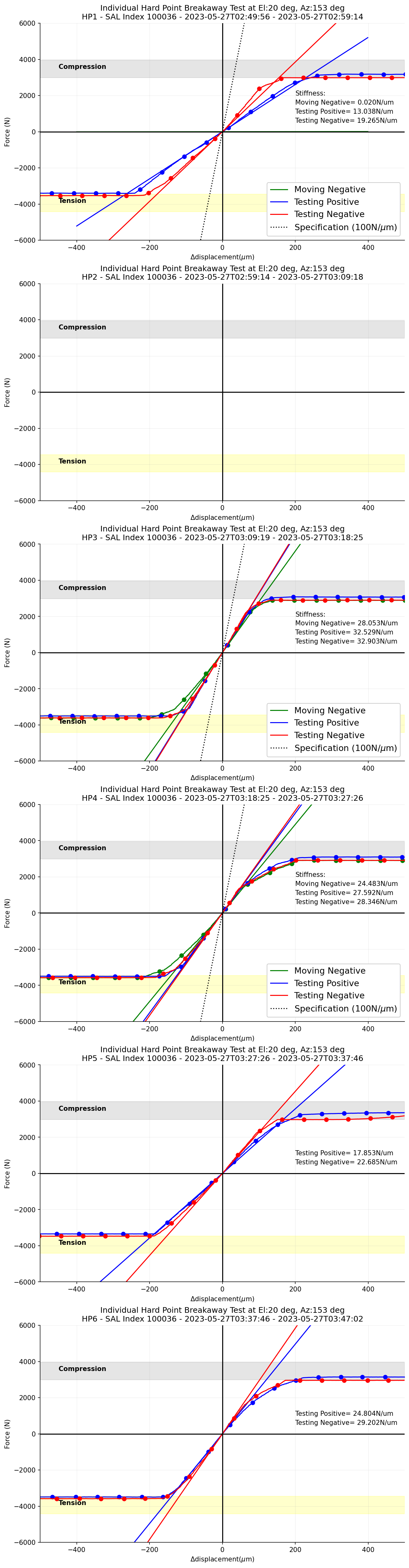
Figure 11 \(\Delta\)Displacement versus measured forces for each phase during the hardpoint breakaway test when the TMA is at el=20 deg.¶
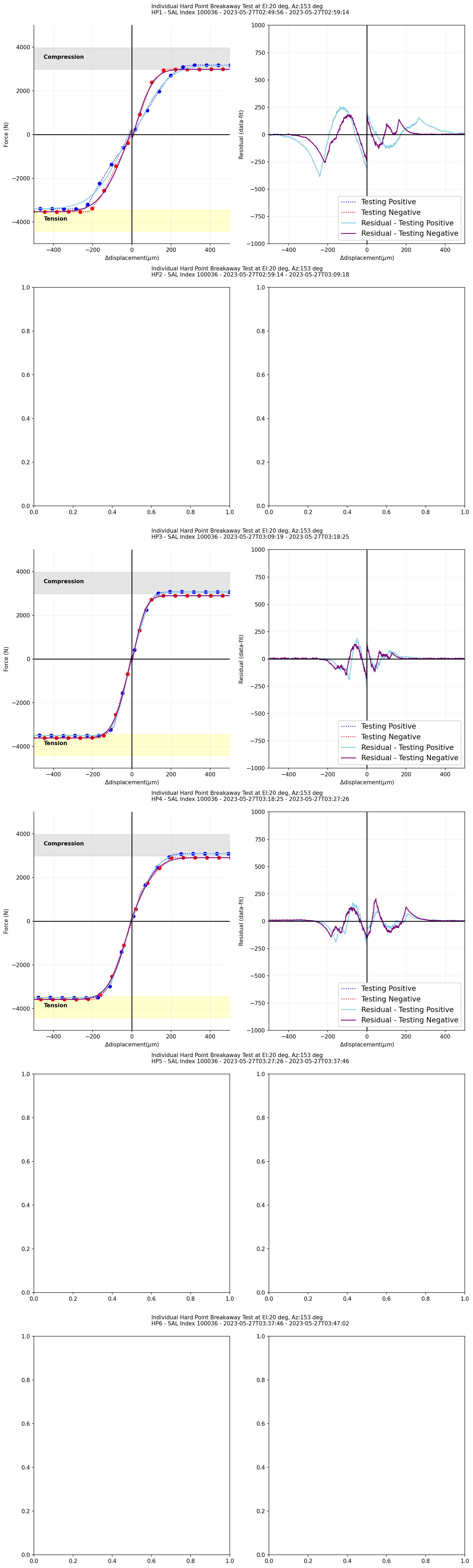
Figure 12 (Left) \(\Delta\)Displacement versus measured forces for each phase during the hardpoint breakaway test fit with error function (the TMA at el=20deg). (Right) The residual, a difference between data and error function, with respect to \(\Delta\)displacement¶
5.6 HP Test at el 10 deg¶
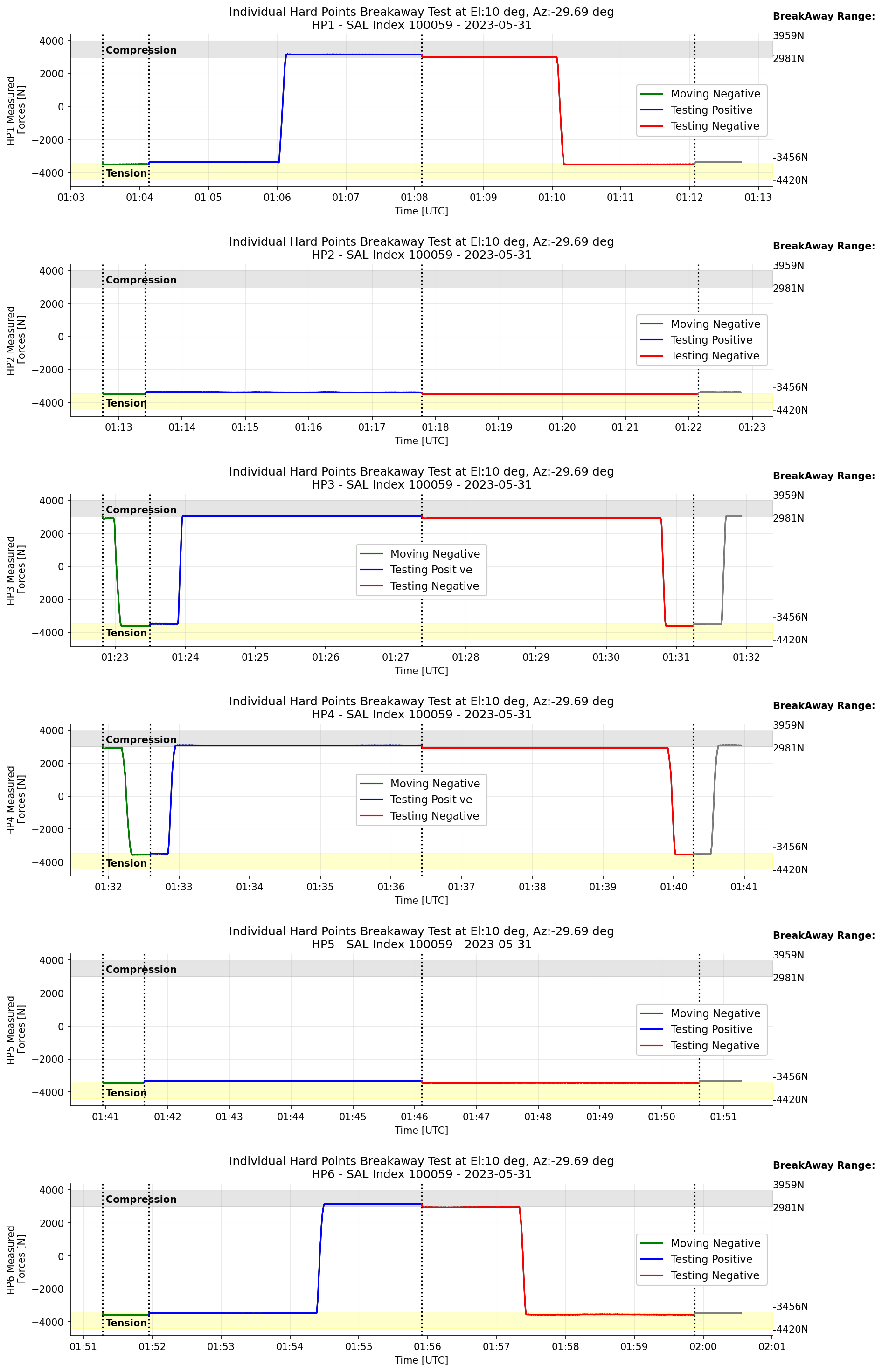
Figure 13 Transition of the measured forces on each hardpoint when the TMA is at el=10deg.¶
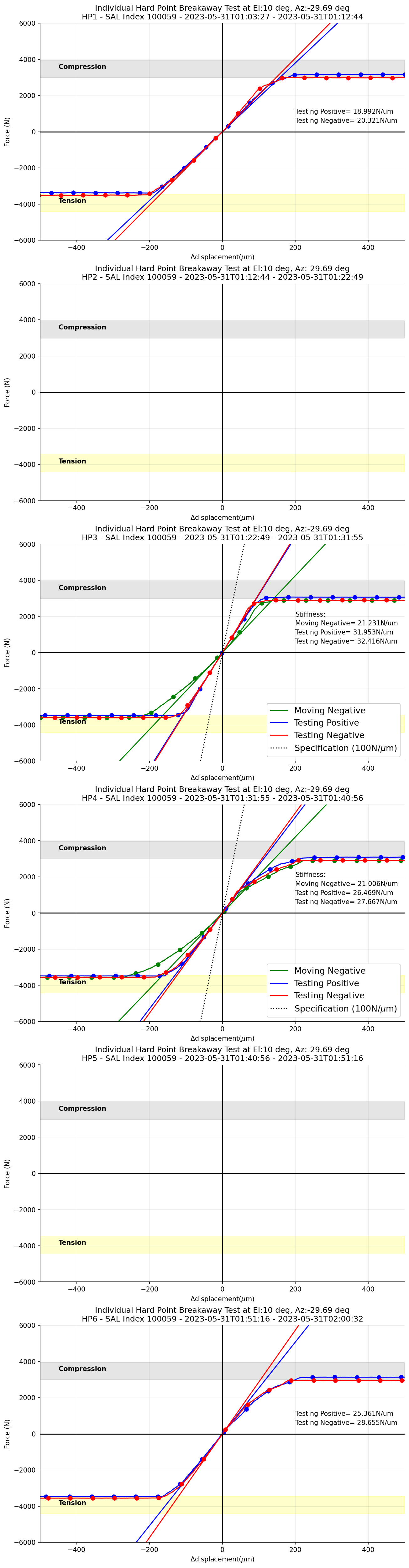
Figure 14 \(\Delta\)Displacement versus measured forces for each phase during the hardpoint breakaway test when the TMA is at el=10 deg.¶
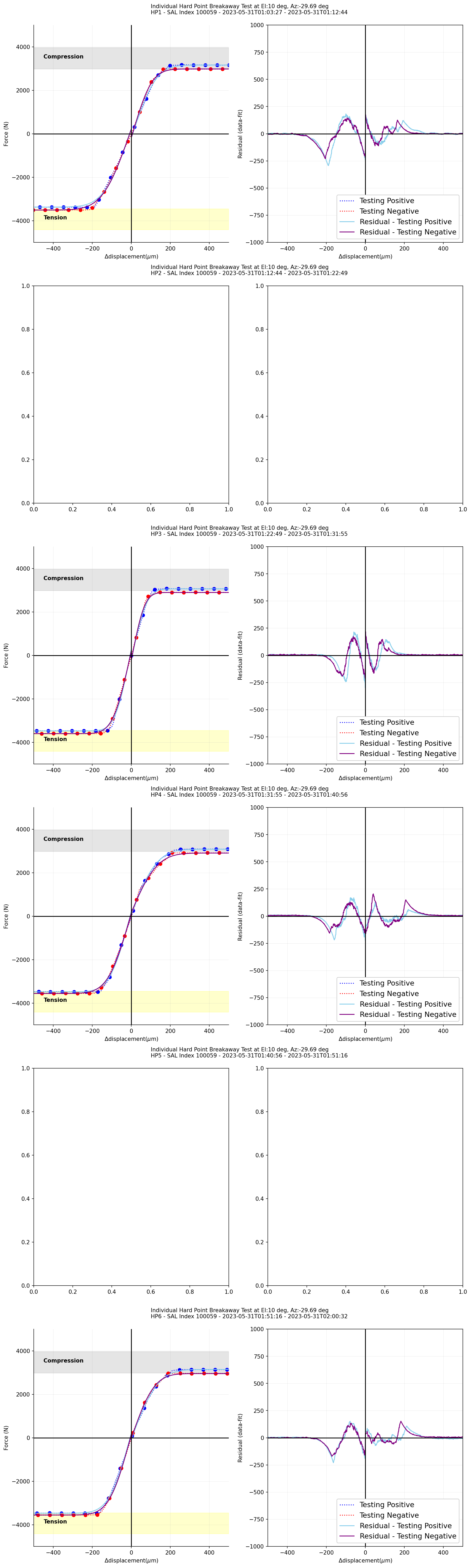
Figure 15 (Left) \(\Delta\)Displacement versus measured forces for each phase during the hardpoint breakaway test fit with error function (the TMA at el=10deg). (Right) The residual, a difference between data and error function, with respect to \(\Delta\)displacement¶
5.7 HP Test at el 5 deg¶
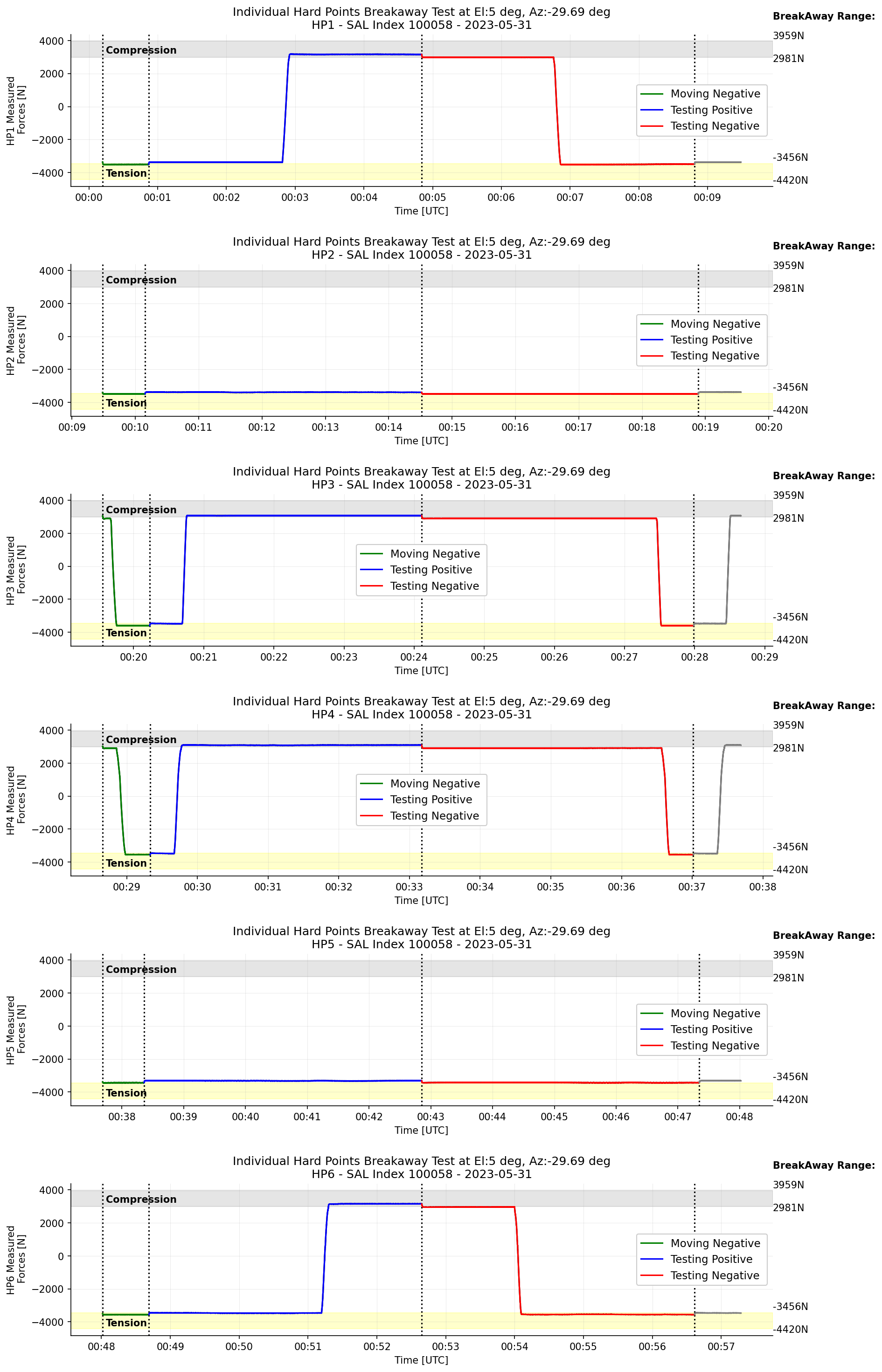
Figure 16 Transition of the measured forces on each hardpoint when the TMA is at el=5deg.¶
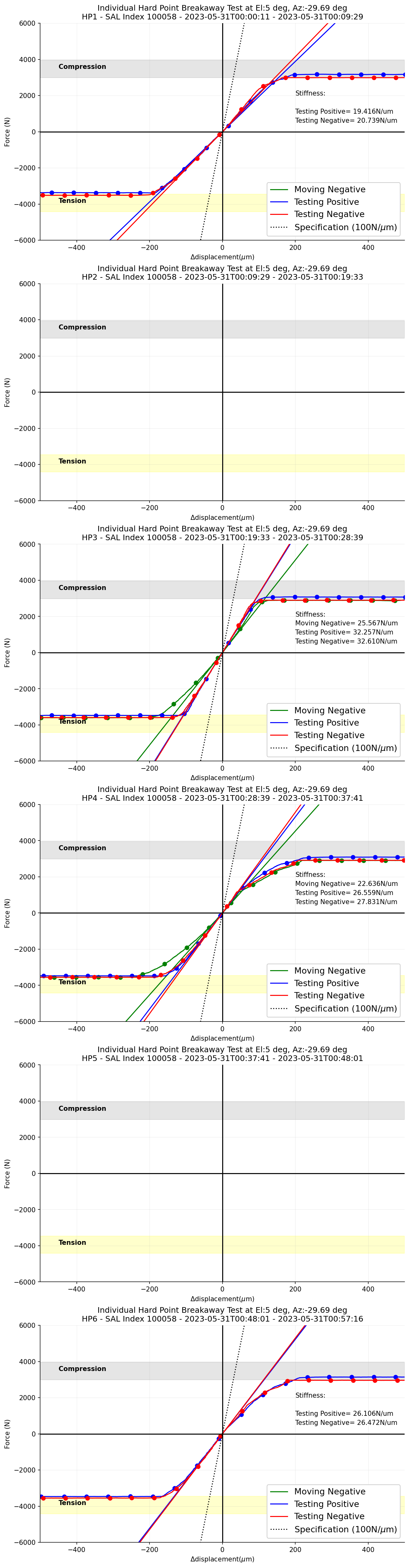
Figure 17 \(\Delta\)Displacement versus measured forces for each phase during the hardpoint breakaway test when the TMA is at el=5 deg.¶
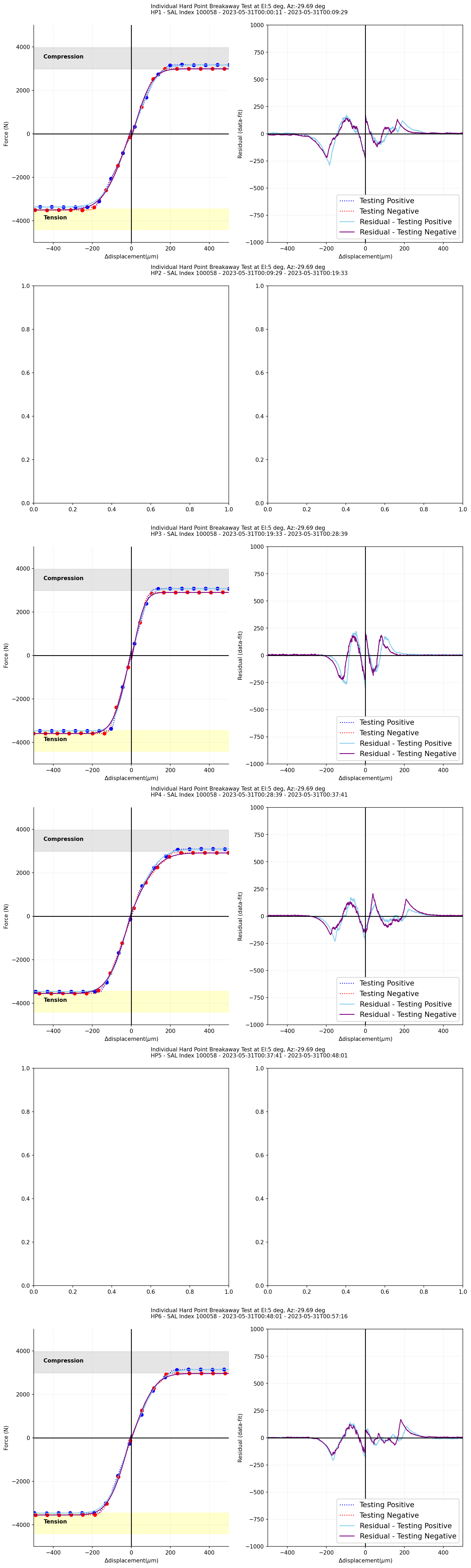
Figure 18 (Left) \(\Delta\)Displacement versus measured forces for each phase during the hardpoint breakaway test fit with error function (the TMA at el=5deg). (Right) The residual, a difference between data and error function, with respect to \(\Delta\)displacement¶
5.8 HP Test at el 1 deg¶
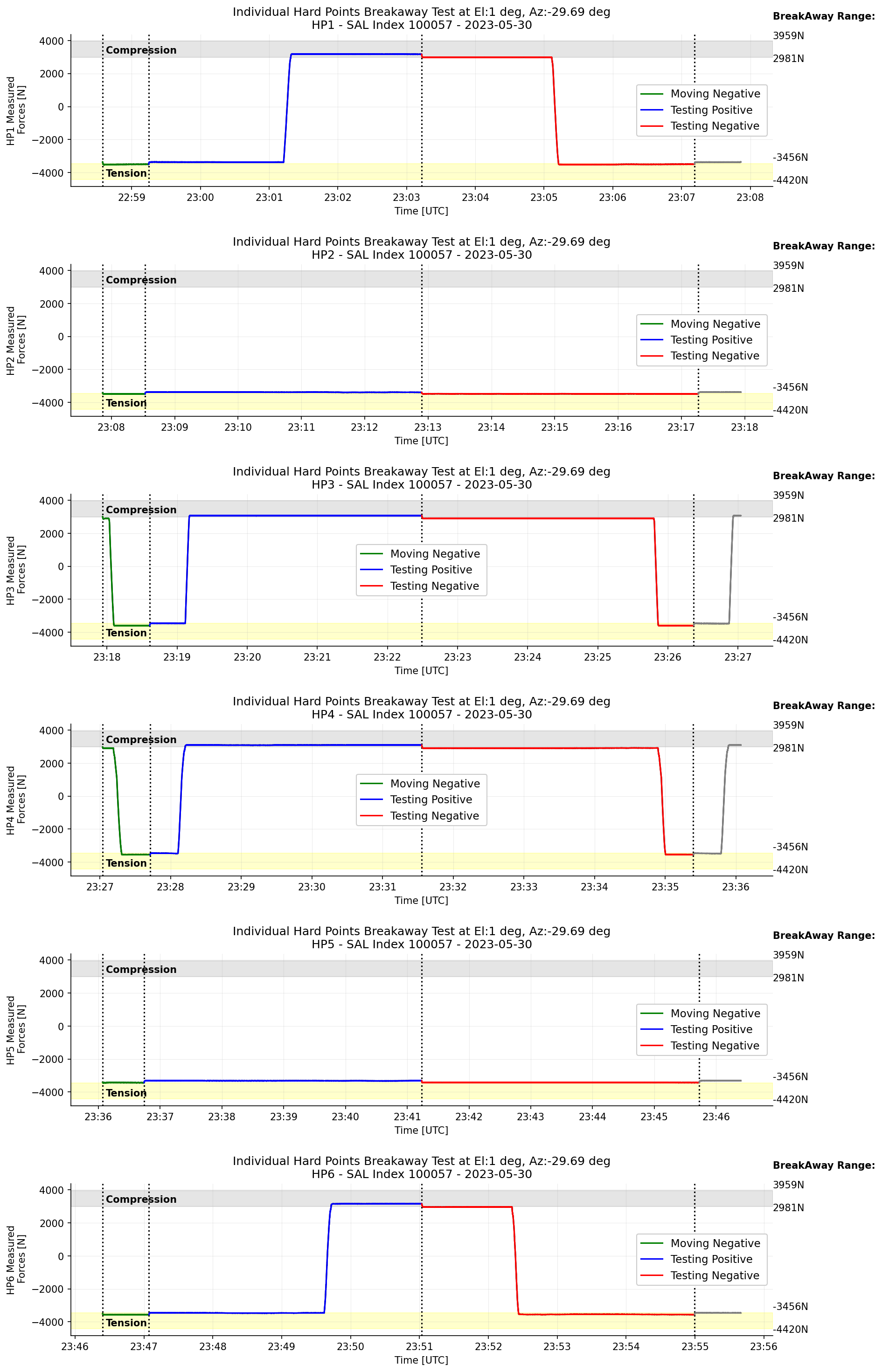
Figure 19 Transition of the measured forces on each hardpoint when the TMA is at el=1deg.¶
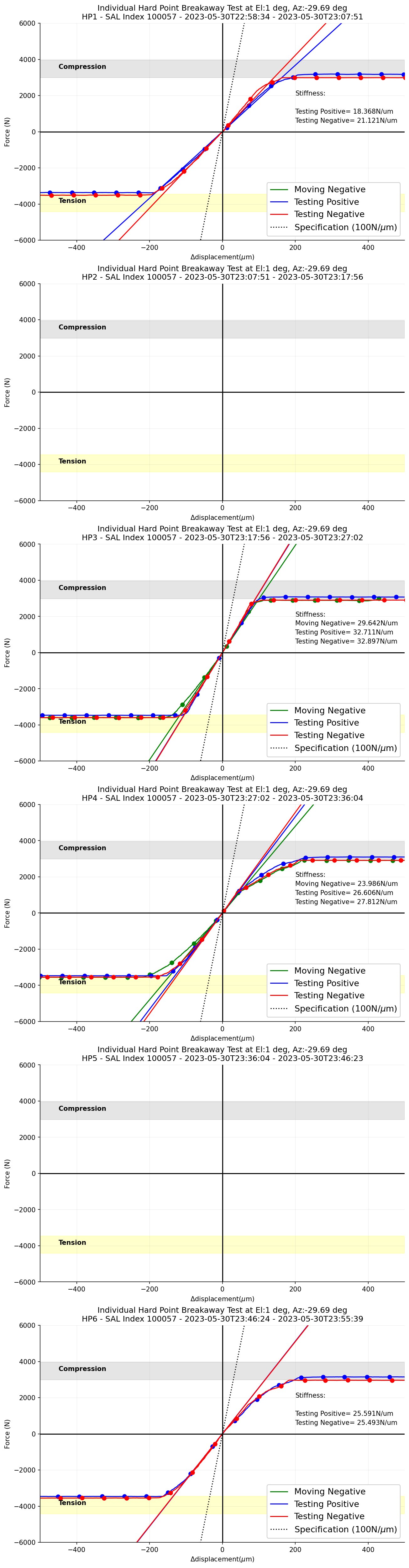
Figure 20 \(\Delta\)Displacement versus measured forces for each phase during the hardpoint breakaway test when the TMA is at el=1 deg.¶
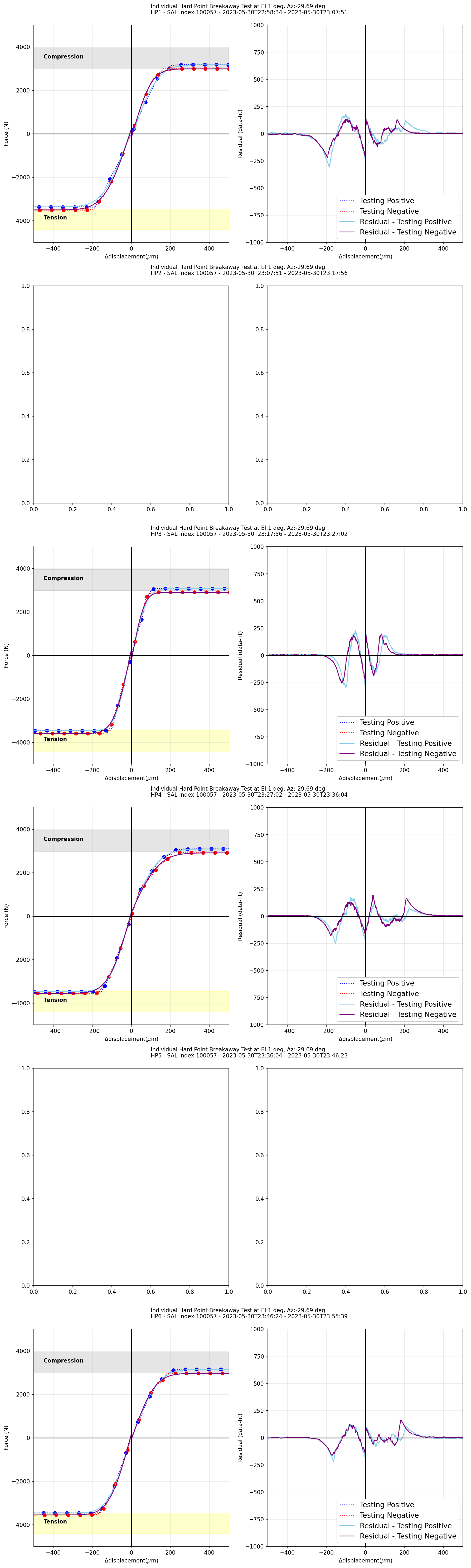
Figure 21 (Left) \(\Delta\)Displacement versus measured forces for each phase during the hardpoint breakaway test fit with error function (the TMA at el=1deg). (Right) The residual, a difference between data and error function, with respect to \(\Delta\)displacement¶
5.9 Requirment discussion¶
References
Felipe Daruich, Douglas Neill, Michael Warner, Edward Hileman, Myung Cho, Christoph Dribusch, Constanza Araujo, Michael Booth, Christopher Contaxis, Ron Harris, Brian Johnson, Garry Knight, Neill Mills, Gary Muller, Edward Stover, Oliver Wiecha, and Bo Xin. LSST M1M3 active mirror support system optimized to accommodate rapid telescope motions. In Heather K. Marshall and Jason Spyromilio, editors, Ground-based and Airborne Telescopes VII, volume 10700 of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, 107003G. July 2018. doi:10.1117/12.2313724.